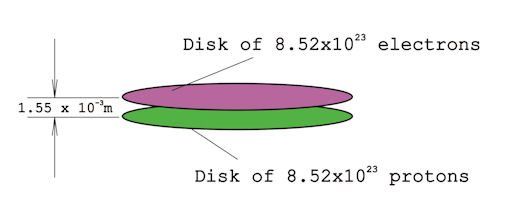
|
Here's something: If you have a concept of the size of an atom, and know that the atomic nucleus is about 10,000 times smaller — with a volume a one-trillionth that of an atom — then you should appreciate how much force it would take to push two uranium nuclei right up against each other. It's slightly less than 2,000 lbs! I happened to calculate this because the question came to mind while I was watching a show about the Large Hadron Collider. I had estimated a millionth of a pound, maybe even on the order of a thousandth of a pound, but, boy, was I surprised. I'm still not convinced my calculation is correct, even after posting it on Physics Forum and asking several physics-trained people about it and getting no objections. Here are some specifics on how I did the calculation: I Googled up "nuclear diameter" and got 15 femtometers (15x10-15 meter) from Wikipedia. Here's a diagram of two uranium nuclei pushed right up against each other: 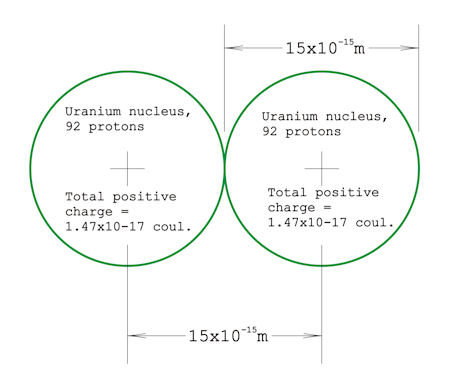
|